Expression Solver

In this section, we describe the basic functionality of the expression solver. This tool has been implemented as a submodule to standardize solving of numerical expression in Physical Units and logical/numerical expressions in Dimensional Input Parameters. For more details and implementation patterns, we refer our reader directly to the source code of the mentioned submodules and corresponding PyTest-s. Nevertheless, it can be easily modified and used in other projects that require some mathematical expressions.

Expression solver consists of the following classes:

Solver

Main class of the solver.

Expression

The expression class handles an expression string that is being parsed into tokens.

Tokens

This class contains a list of parsed tokens (atoms and operators).

Atom

Class that specifies how data is parsed from atomic expressions and implements mathematical operations on the data.

Operators

Each operator (e.g. addition, multiplication, logarithm….) is implemented as a separate class and performs corresponding operations with tokens.

Expression solver comes with a default atom parser that can be used straight out of the box on basic numerical,

>>> from scinumtools.solver import *
>>> with ExpressionSolver(AtomBase) as es:
...     es.solve("1 * ((2+3) / +3 - -10 ) + (-23 *++2) + 23**2")
Atom(494.6666666666667)
>>> 1 * ((2+3) / +3 - -10 ) + (-23 *++2) + 23**2
494.6666666666667

comparison and logical expressions.

>>> import numpy as np
>>> with ExpressionSolver(AtomBase) as es:
...     es.solve("sin(23) < 1 && 3*2 == 6 || !(23 > 43) && cos(0) == 1")
Atom(True)
>>> np.sin(23) < 1 and 3*2 == 6 or not (23 > 43) and np.cos(0) == 1
True

Note

The Expression Solver described in this documentation is currently written in Python. Nevertheless, a C++ implementation is already available on GitHub. This can be currently used only as a standalone library. In the future, it will be incorporated into the ‘scinumtools’ project to boost its efficiency.

Atoms

Atom parser is a central part of every solver, because it converts atomic expression into specific data type and implements operations with the data. Default atom class implements parsing and operation on float numbers. The functionality of the atom can be easily modified, as shown in the example below.

>>> foo = 3
>>> bar = 4
>>> class Atom(AtomBase):
>>>     def __init__(self, value:str):
>>>         if value=='foo':
>>>             self.value = foo
>>>         elif value=='bar':
>>>             self.value = bar
>>>         else:
>>>             self.value = float(value)
>>> with ExpressionSolver(Atom) as es:
>>>     es.solve('foo < bar && foo * bar == 12')
Atom(True)
>>> foo < bar and foo*bar==12
True

Operators

A list of default operations is given in the table below.

List of operators

Name	Abbreviation	Operation
Addition	add	unary +A and binary A+B
Subtraction	sub	unary -A and binary A-B
Multiplication	mul	A*B
Division	truediv	A/B
Parenthesis	par	(E)
Exponential function	pow, exp, powb	A**B, exp(E), powb(E1,E2)
Logarithmic functions	log, log10, logb	log(E), log10(E), logb(E1,E2)
Trigonometric functions	sin, cos, tan	sin(E), cos(E), tan(E)
Equality	eq, ne, lt, gt, le, ge	A==B, A!=B, A<B, A>B, A<=B, A>=B
Logical operators	and, or, not	A&&B, A||B, !B

Symbols A and B used in the table stand for atoms, and E for expressions.

Operators can be easily overloaded or modified to match the needs of your project.

>>> class CustomOperatorNot(OperatorNot):
>>>     symbol: str = 'not'
>>> operators = {'not':CustomOperatorNot}
>>> with ExpressionSolver(AtomBase, operators) as es:
>>>     es.solve('not 1')
False

Operation steps

It is critical, that the operations described above are evaluated in a correct order after each other. The table below summarizes evaluation steps, from first to last, that are implemented in the code.

Operation steps

Type	Operators
parenthesis	log, log10, logb, exp, sqrt, powb, sin, cos, tan, par
unary	add, sub
binary	pow
binary	mul, truediv
binary	add, sub
binary	eq, ne, le, ge, lt, gt
unary	not
binary	and
binary	or

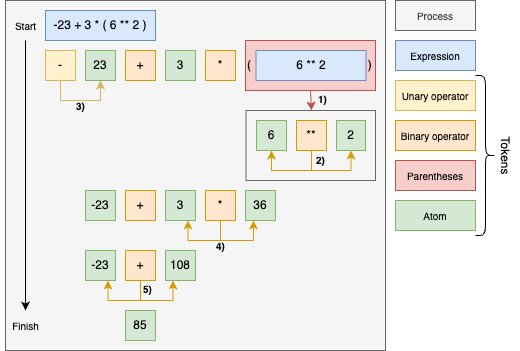
Decomposition of a string expression into tokens and subsequent action of operators on atoms is depicted in the figure below. First, expressions in parentheses 1) are solved in a sub-process 2). In the second step, unary operations 3) are evaluated. After that, binary operations 4) and 5) bring the rest of the expression to the final solution. Logical and comparison operations are not included in the figure, but if used, they are evaluated in the order from the table discussed earlier.

The order of operations can be used as it is, but it can also be modified. In the following example, we introduce entirely new operators and implement their order into a custom operation step sequence.

>>> class OperatorSquare(OperatorBase):   # operate from left side
>>>     symbol: str = '~'
>>>     def operate_unary(self, tokens):
>>>         right = tokens.get_right()
>>>         tokens.put_left(right*right)
>>> class OperatorCube(OperatorBase):     # operate from right side
>>>     symbol: str = '^'
>>>     def operate_unary(self, tokens):
>>>         left = tokens.get_left()
>>>         tokens.put_left(left*left*left)
>>> operators = {'square':OperatorSquare,'cube':OperatorCube,'add':OperatorAdd}
>>> steps = [
>>>     dict(operators=['square','cube'], otype=Otype.UNARY),
>>>     dict(operators=['add'],           otype=Otype.BINARY),
>>> ]
>>> with ExpressionSolver(AtomBase, operators, steps) as es:
>>>     es.solve('~3 + 2^')
Atom(17)

Sometimes also atom class needs to be modified to achieve a desired solution.

>>> class AtomCustom(AtomBase):
>>>     value: str
>>>     def __init__(self, value:str):
>>>         self.value = str(value)
>>>     def __add__(self, other):
>>>         return AtomCustom(self.value + other.value)
>>>     def __gt__(self, other):
>>>         return AtomCustom(len(self.value) > len(other.value))
>>> operators = {'add':OperatorAdd,'gt':OperatorGt,'par':OperatorPar}
>>> steps = [
>>>     dict(operators=['par'],  otype=Otype.ARGS),
>>>     dict(operators=['add'],  otype=Otype.BINARY),
>>>     dict(operators=['gt'],   otype=Otype.BINARY),
>>> ]
>>> with ExpressionSolver(AtomCustom, operators, steps) as es:
>>>     es.solve("(limit + 100 km/s) > (limit + 50000000000 km/s)")
Atom('False')